It’s all got very messy in Leeds.
A long-term strategy of the government, supported in general by the health profession, is the concentration of high-risk uncommon surgery in fewer centres. This of course means closing departments in some hospitals currently providing those services. Few are in doubt that child heart surgery is high-risk, relatively uncommon and there are probably too many UK centres performing this highly specialised surgery at the moment. Leeds was one of three UK hospitals identified in an NHS review where congenital heart surgery would stop.
On this background and a vigorous local campaign, a case was won in the High Court which ruled the consultation flawed. That was 7th March 2013 and the ruling was published 3 days ago.
The following day, children’s heart surgery was suspended at Leeds after NHS Medical Director, Sir Bruce Keogh, was shown data suggesting that the mortality rate in Leeds was higher than expected.
There have been rumblings in the cardiac surgical community for some time that all was not well in Leeds … As medical director I couldn’t do nothing. I was really disturbed about the timing of this. I couldn’t sit back just because the timing was inconvenient, awkward or would look suspicious, as it does.
– Sir Bruce Keogh, NHS Medical Director
An “agitated cardiologist” later identified as Professor Sir Roger Boyle, director of the National Institute of Clinical Outcomes Research, told Sir Bruce that mortality rates over the last two years were “about twice the national average or more” and rising.
These data are not in the public domain. Sir Bruce and the Trust faced a difficult decision given the implications of the data. This is complicated by the recent court ruling and strength of public feeling, the recent publication of the Francis report into Mid Staffordshire NHS Foundation Trust and the background of cardiac surgery deaths at Bristol Royal Infirmary between 1984 and 1995.
Is mortality in Leeds higher than expected? What is expected? How much variation can be put down to chance? Is this how a potential outlier should be managed?
Dr John Gibbs, chairman of the Central Cardiac Database and the man responsible for the collection and analysis of the data has said the data are “not fit to be looked at by anyone outside the committee”.
It was at a very preliminary stage, and we are at the start of a long process to make sure the data was right and the methodology was correct. We would be irresponsible if we didn’t put in every effort to get the data right. It will cause untold damage for the future of audit results in this country. I think nobody will trust us again. It’s dreadful.
– Dr John Gibbs, chairman of the Central Cardiac Database
Not surprisingly, a senior cardiologist from Leeds, Elspeth Brown, has come out and said the data are just plain wrong and did not include all the relevant operations.
Twice the national average sounds a lot. is it?
Possibly. It’s difficult to know not seeing the data. Natural variation between hospitals in the results of surgery can and does occur by chance. It is possible to see “twice the national average” as a results of natural variation, disturbing as that may sound. It depends on the number of procedures performed annually – small hospitals have more variation – and whether all cardiac procedures are compared together, as opposed to each individual surgical procedure in isolation.
The challenge is in confidently detecting hospitals performing worse than would be expected by chance, as has been alleged in Leeds. Care needs to be taken to ensure that data are accurate and complete. Account is usually made of differences in the patients being treated and the complexity of the surgery performed (often referred to as case-mix).
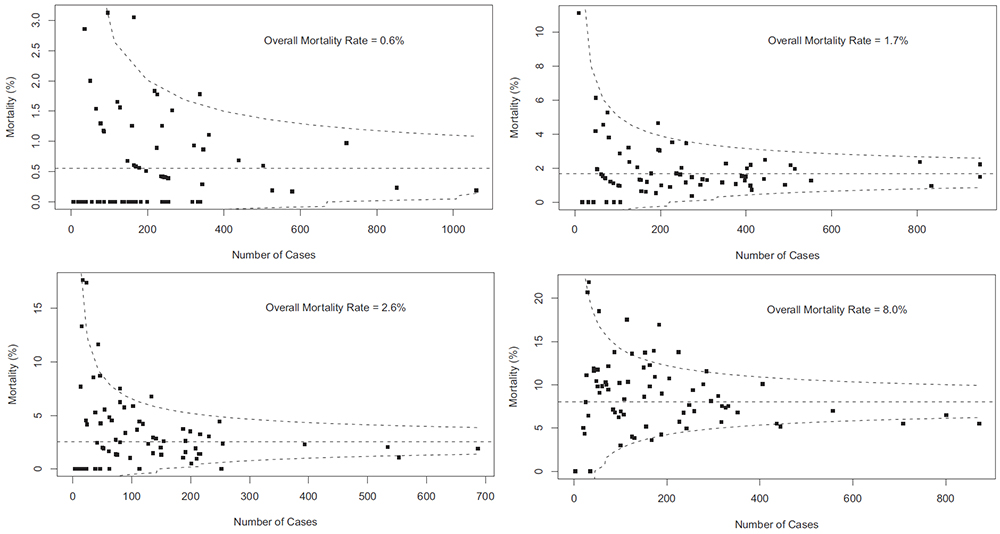
The graphs below are “funnel plots” that show differences in mortality after congenital heart surgery in US hospitals. These were published in 2012 by Jacobs and colleagues from the University of South Florida College of Medicine. The open source paper is here, but the graphs come from the final paper here which although behind a paywall, the graphs are freely available (note the final version differs from the open source version).
Each graph is for group of child heart operations of increasing complexity and therefore risk. Upper left are the more straightforward procedures, bottom right more complex. The horizontal axis is the annual number of cases and the vertical axis the mortality as a percentage. Each dot on the graph is a hospital performing that particular type of surgery. If a hospital lies outwith the dotted line (95% confidence interval) then there is a possibility that the mortality rate is different from the average. The further above the top line, the greater the chance. These particular funnel plots are not corrected for case-mix, but this has been done else where in the analysis.
It is easy to see that when a hospital does few cases per year, the natural variation in mortality can be high. On the first graph, there is variation from 0 – 3% between different hospitals and this range increases as the surgery gets riskier. There is less variation between hospitals that do more cases. However, in the second graph even the two hospitals doing around 800 procedures per year, there is a greater than two-fold difference in mortality. On the first plot, twice the national average is 1.2%. There are around 11 hospitals above that level in the US for these procedures, the differences for 9 apparently occuring by chance (within the dotted line). Similar conclusions can be drawn from the other graphs of increasingly risky surgery.
Data for cardiac sugery is published and freely available to the public. At the moment, data for children’s heart surgery is not published separately. The data for Leeds General Surgery can be seen here.
To compare children’s heart surgery in Leeds with other centres, we need to the raw data presented in this form and the data corrected for differences in patients. Other issues may be at play, but with the data in the public domain we will be in a better position to make a judgement as to whether an excess in mortality does indeed exist.