ProPublica is an organisation performing independent, non-profit investigative journalism in the public interest. Yesterday it published an analysis of surgeon-level complications rates based on Medicare data.
Publication of individual surgeons results is well established in the UK. Transparent, easily accessible healthcare data is essential and initiatives like this are welcomed.
It is important that data are presented in a way that can be clearly understood. Communicating risk is notoriously difficult. This is particularly difficult when it is necessary to describe the precision with which a risk has been estimated.
Unfortunately that is where ProPublica have got it all wrong.
There is an inherent difficulty faced when we dealing with individual surgeon data. In order to be sure that a surgeon has a complication rate higher than average, that surgeon needs to have performed a certain number of that particular procedure. If data are only available on a small number of cases, we can’t be certain whether the surgeon’s complication rate is truly high, or just appears to be high by chance.
If you tossed a coin 10 times and it came up with 7 heads, could you say whether the coin was fair or biased? With only 10 tosses we don’t know.
Similarly, if a surgeon performs 10 operations and has 1 complication, can we sure that their true complication rate is 10%, rather than 5% or 20%? With only 10 operations we don’t know.
The presentation of the ProPublica data is really concerning. Here’s why.
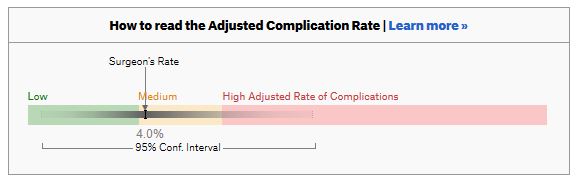
For a given hospital, data are presented for individual surgeons. Bands are provided which define “low”, “medium” and “high” adjusted complication rates. If the adjusted complication rate for an individual surgeon falls within the red-zone, they are described as having a “high adjusted rate of complications”.
How confident can we be that a surgeon in the red-zone truly has a high complication rate? To get a handle on this, we need to turn to an off-putting statistical concept called a “confidence interval”. As it’s name implies, a confidence interval tells us what degree of confidence we can treat the estimated complication rate.
If the surgeon has done many procedures, the confidence interval will be narrow. If we only have data on a few procedures, the confidence interval will be wide.
To be confident that a surgeon has a high complication rate, the 95% confidence interval needs to entirely lie in the red-zone.
A surgeon should be highlighted as having a high complication rate if and only if the confidence interval lies entirely in the red-zone.
Here is an example. This surgeon performs the procedure to remove the gallbladder (cholecystectomy). There are data on 20 procedures for this individual surgeon. The estimated complication rate is 4.7%. But the 95% confidence interval goes from the green-zone all the way to the red-zone. Due to the small number of procedures, all we can conclude is that this surgeon has either a low, medium, or high adjusted complication rate. Not very useful.
Here are some other examples.
Adjusted complication rate: 1.5% on 339 procedures. Surgeon has low or medium complication rate. They are unlikely to have a high complication rate.
Adjusted complication rate: 4.0% on 30 procedures. Surgeon has low or medium or high complication rate. Note due to the low numbers of cases, the analysis correctly suggests an estimated complication rate, despite the fact this surgeon has not had any complications for the 30 procedures.
Adjusted complication rate: 5.4% on 21 procedures. ProPublica conclusion: surgeon has high adjusted complication rate. Actual conclusion: surgeon has low, medium or high complication rate.
Adjusted complication rate: 6.6% on 22 procedures. ProPublica conclusion: surgeon has high adjusted complication rate. Actual conclusion: surgeon has medium or high complication rate, but is unlikely to have a low complication rate.
Adjusted complication rate: 7.6% on 86 procedures. ProPublica conclusion: surgeon has high adjusted complication rate. Actual conclusion: surgeon has high complication rate. This is one of the few examples in the dataset, where the analysis suggest this surgeon does have a high likelihood of having a high complication rate.
In the UK, only this last example would to highlighted as concerning. That is because we have no idea whether surgeons who happen to fall into the red-zone are truly different to average.
The analysis above does not deal with issues others have highlighted: that this is Medicare data only, that important data may be missing , that the adjustment for patient case mix may be inadequate, and that the complications rates seem different to what would be expected.
ProPublica have not moderated the language used in reporting these data. My view is that the data are being misrepresented.
ProPublica should highlight cases like the last mentioned above. For all the others, all that can be concluded is that there are too few cases to be able to make a judgement on whether the surgeon’s complication rate is different to average.
It appears that you have done an accurate reading of our website and the way we presented our information. You have quite clearly seen that we have expressed the confidence intervals in our analysis, which are important to interpreting the results. We have carefully moderated the language in reporting the data, and the data is being represented fairly. You yourself were able to understand it, so it seems that you are making the point. The Adjusted Complication Rate is, however, the most likely place within the confidence interval, so that’s why the results are presented as they are. Thank you for your interest in our work. Many experts have endorsed it, and some have not. You can read their comments at the following link. We invite you and other experts to leave comments here too: https://www.propublica.org/article/surgeon-level-risk-quotes.
“You yourself were able to understand it, so it seems that you are making the point.”
Mr. Marshall, are you under the impression that Dr. Allen is representative of your average reader in terms of his grasp of the analysis and reporting of biostatistics? If so, then his point is made all the more strongly because, I assure you, the average reader does not understand confidence intervals, and is therefore very likely to believe that the data point you present and the band it’s located in represents statistical “fact.” (I know many colleague physicians who struggle with these nuances of biostatistics, so I speak from some perspective on this.) In fact, your follow-up editorial comment on your site, which amounts to “some data is better than no data,” indicates that you continue to miss the point. Bad data, which is what you are in most cases offering on your site, is in fact worse than no data because it misleads and leads to mistakenly confident decision making.
Apologies. That should have read “Mr. Allen” and “Dr. Harrison” in my first line. Sorry for the confusion.
Thank you for the reply.
Please can you publish the number of surgeons with statistically higher complication rates. How many are there?
The data are not represented fairly:
“At least one surgeon performing this procedure has a high adjusted rate of complications.”
In most instances, this statement is demonstrably false as there is no statistical difference.
Similarly:
“Half of all hospitals in America have surgeons with low and high complication rates”.
But not statistically significantly lower or higher in most cases.
This is not semantics. Unfortunately it is not possible to just ignore the statistical analysis when making summary statements.
Ewen, as you can see from the lack of comments here and the comments on propublica the validity of the analysis appears to be of little to no interest to the general public. Although you raise one of the most important issues regarding this, if not the most important, it thus far appears to have fallen on deaf ears. Is false analysis more harmful than none at all? I would say so.
I would also look into how the adjustment was made for the outcome. If it is coming from a model (in this case, ideal is random effects model) which takes into account of physician, and patient-level factors, i.e., number of patients, etc, then I would say taking a funnel-plot approach to validate the outcome is an overkill. Funnel plot is a good approach to see whether a complication rate falls out of accepted range. But we need a model that tells us what factors influenced this complication rate, and are they solely attributable to physician (i.e., how he performed surgeries). In their methodology, Propublica mentioned “We used accepted statistical methods to adjust for age, the health of each patient, luck, and the overall performance of each hospital”, so it is very clear what they have done. Often, we have minimal data to answer complex questions, and this is one of those instances!
Thanks John.
You have probably seen the details of the methodology and appendicies.
As you say, random effects models have been used and the surgeon-level random effects estimates for gallbladder surgery are presented on page 46 of the latter.
No surgeon has a complication rate statistically different to the average (at the 5% level). This is to be expected. To be able to determine this more cases would be needed.
Unfortunately for this analysis, the minimal data is insufficient to answer this complex question!