ProPublica, an independent investigative journalism organisation, have published surgeon-level complications rates based on Medicare data. I have already highlighted problems with the reporting of the data: surgeons are described as having a “high adjusted rate of complications” if they fall in the red-zone, despite there being too little data to say whether this has happened by chance.

I say again, I fully support transparency and public access to healthcare. But the ProPublica reporting has been quite shocking. I’m not aware of them publishing the number of surgeons out of the 17000 that are statistically different to the average. This is a small handful.
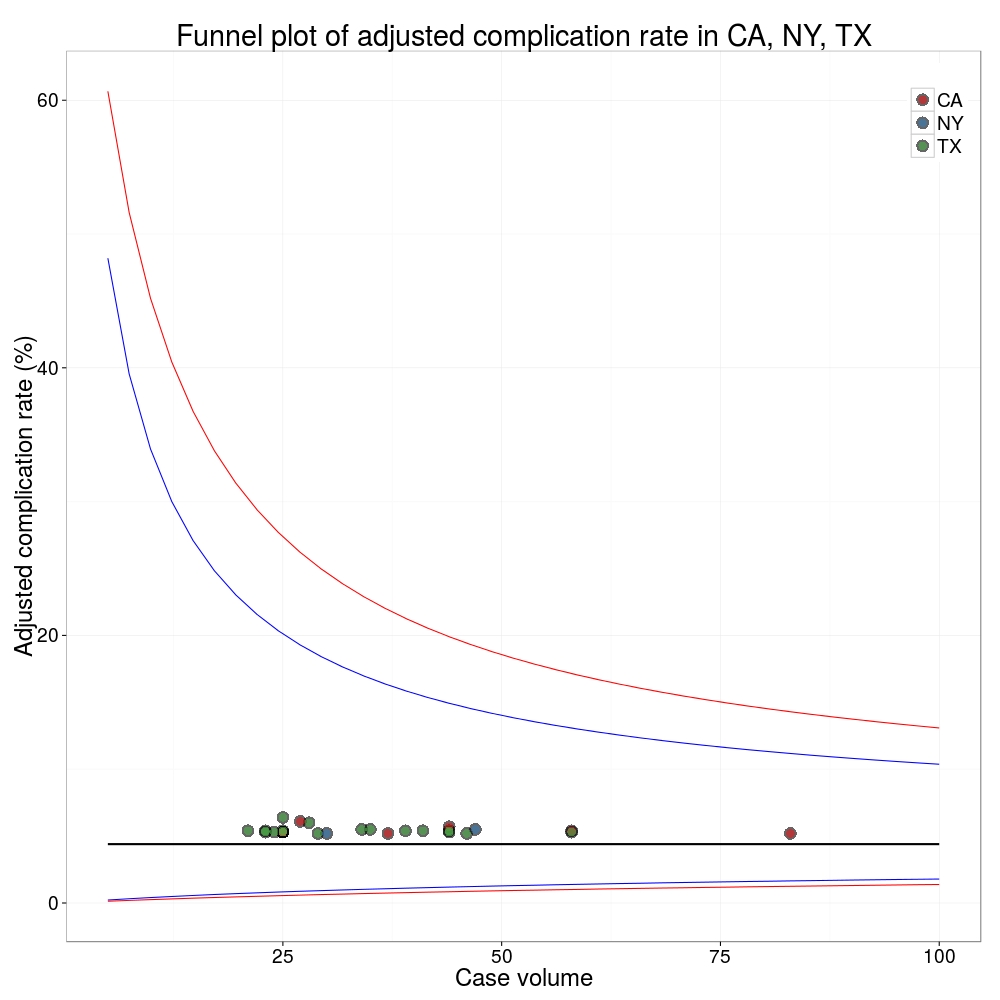
ProPublica could have chosen a different approach. This is a funnel plot and I’ve written about them before.
A funnel plot is a summary of an estimate (such as complication rate) against a measure of the precision of that estimate. In the context of healthcare, a centre or individual outcome is often plotted against patient volume. A horizontal line parallel to the x-axis represents the outcome for the entire population and outcomes for individual surgeons are displayed as points around this. This allows a comparison of individuals with that of the population average, while accounting for the increasing certainty surrounding that outcome as the sample size increases. Limits can be determined, beyond which the chances of getting an individual outcome are low if that individual were really part of the whole population.
In other words, a surgeon above the line has a complication rate different to the average.
I’ve scraped the ProPublica data for gallbladder removal (laparoscopic cholecystectomy) from California, New York and Texas for surgeons highlighted in the red-zone. These are surgeons ProPublica says have high complication rates.
As can be seen from the funnel plot, these surgeons are no where near being outliers. There is insufficient information to say whether any of them are different to average. ProPublica decided to ignore the imprecision with which the complication rates are determined. For red-zone surgeons from these 3 states, none of them have complication rates different to average.
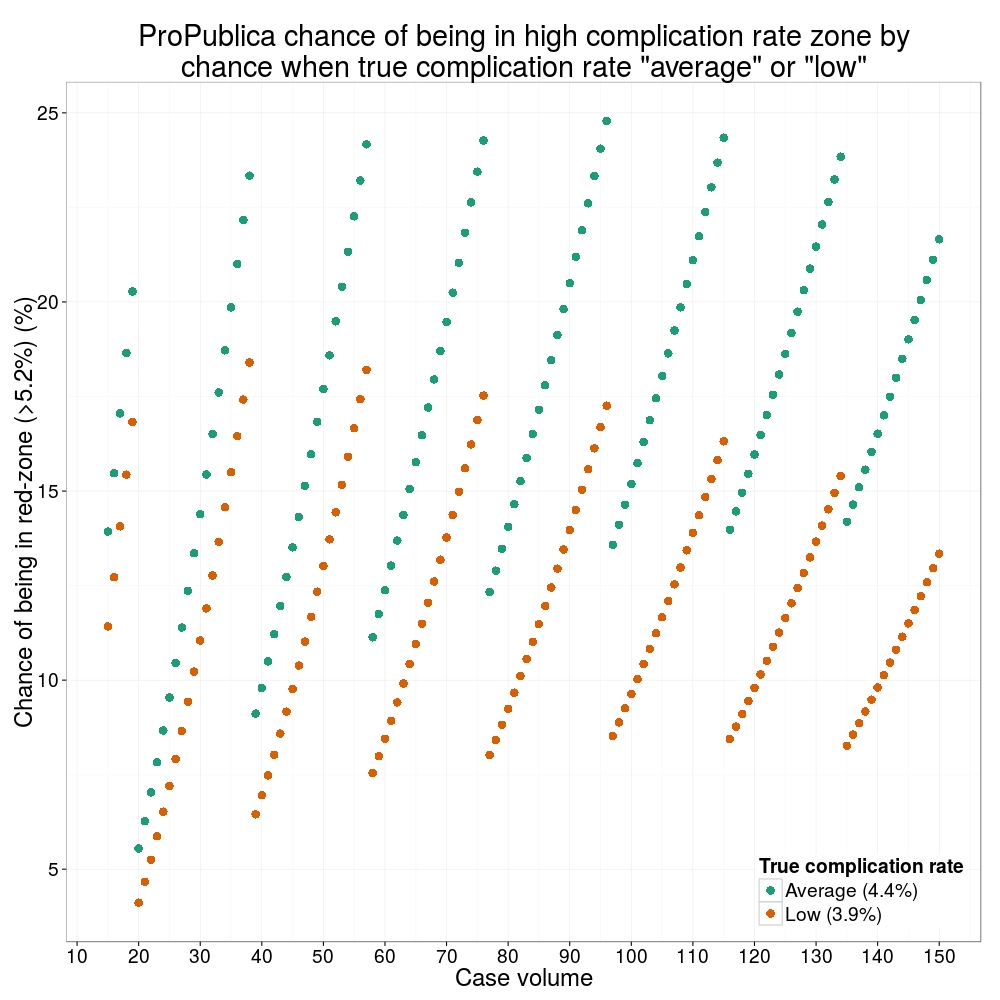
How likely is it that a surgeon with an average complication rate (4.4%) will appear in the red-zone just by chance (>5.2%)? The answer is, pretty likely given the small numbers of cases here: anything up to a 25% chance depending on the number of cases performed. Even at the top of the green-zone (low ACR, 3.9%), there is still around a 1 in 6 chance a surgeon will appear to have a high complication rate just by chance.
 ProPublica have failed in their duty to explain these data in a way that can be understood. The surgeon score card should be revised. All “warning explanation points” should be removed for those other than the truly outlying cases.
ProPublica have failed in their duty to explain these data in a way that can be understood. The surgeon score card should be revised. All “warning explanation points” should be removed for those other than the truly outlying cases.
Data
Git
Code
# ProPublica Surgeon Scorecard
# https://projects.propublica.org/surgeons
# Laparoscopic cholecystectomy (gallbladder removal) data
# Surgeons with "high adjusted rate of complications"
# CA, NY, TX only
# Libraries needed ----
library(ggplot2)
library(binom)
# Upload dataframe ----
dat = read.csv("http://www.datasurg.net/wp-content/uploads/2015/07/ProPublica_CA_NY_TX.csv")
# Total number reported
dim(dat)[1] # 59
# Remove duplicate surgeons who operate in more than one hospital
duplicates = which(
duplicated(dat$Surgeon)
)
dat_unique = dat[-duplicates,]
dim(dat_unique) # 27
# Funnel plot for gallbladder removal adjusted complication rate -------------------------
# Set up blank funnel plot ----
# Set control limits
pop.rate = 0.044 # Mean population ACR, 4.4%
binom_n = seq(5, 100, length.out=40)
ci.90 = binom.confint(pop.rate*binom_n, binom_n, conf.level = 0.90, methods = "wilson")
ci.95 = binom.confint(pop.rate*binom_n, binom_n, conf.level = 0.95, methods = "wilson")
ci.99 = binom.confint(pop.rate*binom_n, binom_n, conf.level = 0.99, methods = "wilson")
theme_set(theme_bw(24))
g1 = ggplot()+
geom_line(data=ci.95, aes(ci.95$n, ci.95$lower*100), colour = "blue")+
geom_line(data=ci.95, aes(ci.95$n, ci.95$upper*100), colour = "blue")+
geom_line(data=ci.99, aes(ci.99$n, ci.99$lower*100), colour = "red")+
geom_line(data=ci.99, aes(ci.99$n, ci.99$upper*100), colour = "red")+
geom_line(aes(x=ci.90$n, y=pop.rate*100), colour="black", size=1)+
xlab("Case volume")+
ylab("Adjusted complication rate (%)")+
scale_colour_brewer("", type = "qual", palette = 6)+
theme(legend.justification=c(1,1), legend.position=c(1,1))
g1
g1 +
geom_point(data=dat_unique, aes(x=Volume, y=ACR), colour="black", alpha=0.6, size = 6,
show_guide=TRUE)+
geom_point(data=dat_unique, aes(x=Volume, y=ACR, colour=State), alpha=0.6, size=4) +
ggtitle("Funnel plot of adjusted complication rate in CA, NY, TX")
# Probability of being shown as having high complication rate ----
# At 4.4%, what are the changes of being 5.2% by chance?
n <- seq(15, 150, 1)
average = 1-pbinom(ceiling(n*0.052), n, 0.044)
low = 1-pbinom(ceiling(n*0.052), n, 0.039)
dat_prob = data.frame(n, average, low)
ggplot(melt(dat_prob, id="n"))+
geom_point(aes(x=n, y=value*100, colour=variable), size=4)+
scale_x_continuous("Case volume", breaks=seq(10, 150, 10))+
ylab("Adjusted complication rate (%)")+
scale_colour_brewer("True complication rate", type="qual", palette = 2, labels=c("Average (4.4%)", "Low (3.9%)"))+
ggtitle("ProPublica chance of being in high complication rate zone by\nchance when true complication rate \"average\" or \"low\"")+
theme(legend.position=c(1,0), legend.justification=c(1,0))


Hi! I was involved in some of the statistical programming for Surgeon Scorecard.
The standard that we used for labeling a high complication rate is that the best point estimate was above a given threshold.
You correctly point out that this is different than requiring p<0.05, or (similarly, but not quite equivalently) having the 95% confidence interval entirely in the red zone. The point of that would be to control the false positive rate.
But what about the false negative rate? From the patient's point of view, why not insist on 95% certainty that the doctor does NOT have a higher than average complication rate before labeling them in the yellow "medium" zone? You could draw equivalent funnel plots for surgeons classified as "medium" and ask how often we could expect them to actually be "high" risk.
Classifying based on the best point estimate is essentially a "more likely than not" classification that balances the harm of false positives vs false negatives — or to put it another way, the interests of surgeons vs. patients.
Hi Jonathan,
Thank you for taking the time to reply, it is useful to have your input.
I agree, the ProPublica data for gallbladder disease has too few cases per surgeon to say any has a low complication rate. For most included surgeons doing gallbladder surgery, nothing can be concluded about their complication rate. Nothing at all. That’s the conclusion of the analysis.
There may be surgeons who appear to have a low or medium complication rate on Surgeonscorecard, who actually have a very high complication rate. As you say, false negatives. This is very important, but we wouldn’t know based on the included gallbladder data.
To draw a firm conclusion from a point-estimate and ignore the distribution from which it is drawn is not credible. I’m surprised anyone with mathematical training would say otherwise.
You will know (but others might not) that on tossing a coin 10 times there is a 38% chance of getting a number of heads other than 5.* So in that simple example, there is a 38% chance of concluding that a normal coin is biased. Doesn’t seem like a sound way to do business.
Lastly, I can’t see published the average number of cases per surgeon. In my gallbladder subset it is 36.
So an average surgeon with 36 included cases has one unfortunate patient who is readmitted to hospital with a wound infection, 1/36 = 2.8% complication rate.
A different surgeon has two patients unfortunate enough to get a wound infection, 2/36 = 5.6% complication rate.
The first is lauded for excellent care, while the second is identified as “more likely than not” being a dangerous surgeon.
While the modelling will move these estimates towards a grand mean, the low case volume problem remains.
*R: n=10; 1-pbinom(n/2, n, 0.5)
The adjusted complication rate is not the raw rate. So your coin flip examples and calculations using the binomial distribution are not correct. We compute the rate as follows:
– build a mixed effects model taking into account fixed effects for age, sex, health, etc. and random effects for surgeon and hospital
– for each surgeon, run the model on the entire patient pool assuming average hospital effect, and compute the complication rate as if this surgeon operated on all patients
This model shows significant shrinkage, that is, high raw rates are moved down toward the mean and low raw rates (including zero observed complications) are moved up toward mean. Here’s a visualization of how shrinkage works, which you will note is quite similar to the figure in our methodology paper: http://www.coppelia.io/2013/08/visualising-shrinkage/
In effect, we are accounting for luck by moving high observed rates in small samples back towards the average, more so with small samples — like your example of 2/36 complications. For some surgeons this shrinkage reduces the rate by 3 or 4 times.
Thanks Jonathan.
It is important to point out to those reading this that your analysis is a standard approach. We published our first hierarchical analysis 4 years ago and most health-services researchers will use mixed models with hospital or healthcare provider as a random effect for these analyses. They are well described in the general surgical literature.
I’d be interested in why you chose a logit-normal model, rather than the more standard logistic model approach?
But really this is all beside the point. For gallbladder disease, the caterpillar plot in your appendices shows no surgeon is different to the mean at the 5% significance level. We would make progress if someone from ProPublica acknowledged that.
You do touch on an interesting question. Should the threshold for triggering identification as an outlier be lowered to increase the true detection rate (sensitivity), at the expense of more false positives? This is a genuinely interesting question which ProPublica could have chosen to lead, rather than going for the approach taken.
Actually I think there are cases in that plot where we have >95% different from median, though you are right that most surgeons rated “high” have the median within the 95% CI. (I’m also looking at a better charts — unfortunately the ones in the current version of the appendix PDF were generated from rounded data and lose the fine detail; this will be updated soon.)
But there are certainly plenty of surgeons greater than 1 SD from the median after shrinkage, for every procedure. So again, why is trying to control the false positive to 5% the correct choice here? It seems to me that the effect of a false positive is limited to an awkward conversation with a surgeon. The effect of a false negative is potentially much worse.
I can’t speak to why logit-normal over logisitic, that was a choice made by Sebastien Haneuse at Harvard, who led the methodology design, and I’m not sure his reasoning on this.
If only it were the case that the effect of a false positive was limited to an awkward conversation. It usually results in the suspension of an individual or in the case of a hospital, a whole service. With the latter, there is the potential for patient harm to occur.
Remember we are talking about false positives here. Individuals or hospitals operating within an “expected range” but falling out with that range due to sampling error.
I sometimes use airport baggage screening as an analogy.
The Transportation Security Administration estimates that each percentage point of the current false alarm rate (about 20%) costs the government tens of millions of dollars per year.
Due the serious implication of missing a bomb (the worst kind of a false negative), the sensitivity/specificity balance is reversed to maximise true positives at the expense of the false positive rate, which is typically set at 20%. Human screeners must resolve alarms raised by the x-ray machine through a combination of repeat scanning, manual search and further tests such as explosive trace-detection screening. In medicine, a cut-off could be chosen which maximises the sensitivity and specificity of the test to detect a specified increase in the rate of the negative outcome, similar to any diagnostic test. In a manner akin to the airport x-ray, this will increase the sensitivity to detect true outliers, but at the expense of an increase in the false positive rate. While in the airport, the consequence of being a false positive is no more than having your bag searched and a slight increase in time getting through security, the same is not the case in medicine. Hospitals or individuals that find themselves on the wrong side of the line, sometimes just by chance, are often judged deficient before any confirmatory process has even started.
As a society we may be able to get to a position where “triggering” is common – an everyday part of reflective practice that a hospital or surgeon may expect to happen every couple of years – and that for the majority, additional scrutiny will show that their practice is not divergent, that they were a false positive. I think healthcare providers would gladly adopt this to increase the likelihood of detecting true outliers.
But as the ProPublica publication has demonstrated, when the practice of an individual is questioned, the reaction of the press and certain sections of society is to cry foul and immediately claim harm has been caused.
Do you really think a surgeon is going to be suspended over their rating in Surgeon Scorecard? Wouldn’t a hospital conduct their own investigation first, using their own more accurate clinical data?
And shouldn’t they be tracking outcomes using their own data anyway? Because most hospitals do not. For example the NSQIP is a better metric, based on clinical data, and 600 hospitals use it to track outcomes… while 3000 do not. (See e.g. https://blogs.sph.harvard.edu/ashish-jha/the-propublica-report-card-a-step-in-the-right-direction/)
Can I turn it round, do you think any surgeons should be suspended on the basis of the ProPublica analysis?
That a hospital participates in NSQIP seems to be insufficient in itself to improve outcomes. At least here:
http://www.ncbi.nlm.nih.gov/m/pubmed/25647205/
Which makes sense. Measurement is not enough if the results are not considered and acted upon.
Collaboration between surgeons and hospitals helps improvement. The building of trust in the early days of collaboration is important. Trust in data sharing and sharing quality improvement strategies.
Where does the public release of outcome data fit into that? I’m not sure. We had a famous incident of a politician stating that it was completely unacceptable that half of hospitals were below average.
From the blog you referenced:
“The right question is – will it leave Bobby better off? I think it will. Instead of choosing based on a sample size of one (his buddy who also had lung surgery), he might choose based on sample size of 40 or 60 or 80. Not perfect. Large confidence intervals? Sure. Lots of noise? Yup. Inadequate risk-adjustment? Absolutely. But, better than nothing? Yes. A lot better.”
As things stand, this is where I disagree. Bobby is currently not better off.
Hello Ewen,
I’m going to ignore the topic entirely and instead point out that the control limits on your funnel plot are incorrect: methods designed for making statements about the population mean based on the sample mean don’t work well in the other direction. You need to work backwards a bit instead, and perhaps take account of the discrete nature of the sample data (to get some really interesting and spiky `funnels’).
That said, it works well enough for a blogpost.
Yours pedantically,
Matt
Hi Matt, nice to hear from you! Hope all is well and things are getting written!
Interested in your line of thinking. The funnel plot control limits here are produced in a standard manner based on a population mean and as you know are simply represent the sampling distribution around that mean. Just as how Public Health England would do them 🙂 http://www.apho.org.uk/default.aspx?RID=39403
However, they are definitely not correct for the purpose they are used for here, as the points are random effects estimates and so are shrunk towards the mean. With the full model, control limits could be simulated. More broadly, comparing the individuals to a population mean is probably not useful anyway. Have now got a full Bayesian model working with cross validation that is probably a more robust way of identifying divergent practice. Coming to a dissertation near you!
Indeed, the APHO ones are also incorrect… they work OK for reasonable proportions and large underlying numbers (>100 population, say), but fail quite badly on edge cases. Basically, on your plot the upper limit is too high, and the lower limits should be at 0% for the whole plot. The easy way to check is to do a thousand or so draws from a binomial distribution with the right mean, and compare with the funnel plot limits. A lot more than 5% will be outside the control limits.
You can see this in the standard Spiegelhalter paper – http://www.medicine.cf.ac.uk/media/filer_public/2010/10/11/journal_club_-_spiegelhalter_stats_in_med_funnel_plots.pdf – particularly Figure 2 on page 1187. Spiegelhalter basically works backwards from exact binomial confidence intervals to define the control limits, while the APHO tool simply uses Wilson score confidence intervals.
The problem, as you do know, is that a CI is a statement of uncertainty about the population mean given the sample mean. Not, in general, the other way round.
The APHO spreadsheet is quite widely used, and so far our efforts to get it updated have not come to anything. One of my colleagues has been working on post-operative mortality, so she’s been putting a bit more effort into getting the APHO spreadsheet corrected; we even have a replacement Excel spreadsheet as of a couple of weeks ago. Now we just need to continue convincing other people until we can get it corrected.
A comparison with binomial limits might still be interesting, but certainly the more appropriate comparison would come from the model. Comparing to the overall mean is probably daft. If the model were fully adjusting for everything appropriately (in some magic manner), then comparing to carefully chosen target values could be interesting.
Aargh dissertations – actually, I’m also not too far off track myself, though it’s not quite as exciting as that.